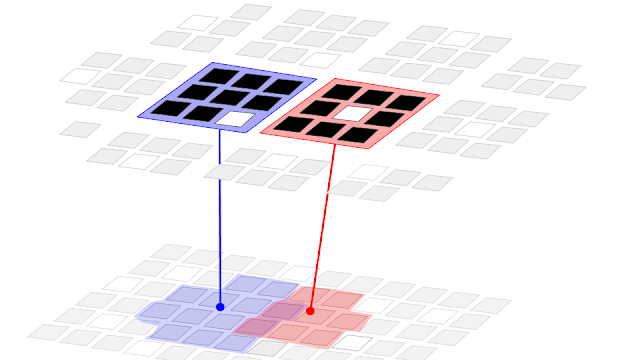
Region-Layer component. The objective is to understand to what extent these ideas work, and to expose limitations both in implementation and theory.
Results will be posted to the blog and written up for publication if, or when, we reach an acceptable level of novelty and rigor.
We are not trying to beat benchmarks here. We’re trying to show whether certain ideas have useful qualities - the best way to tackle specific AI problems is almost certainly not an AGI way. But what we’d love to see is that AGI-inspired methods can perform close to state-of-the-art (e.g. deep convolutional networks) on a wide range of problems. Now that would be general intelligence!
The good thing about MNIST is that it’s simple and has been extremely widely studied. It’s easy to work with the data and the images are a practical size - big enough to be interesting, but not so big as to require lots of preprocessing or too much memory. Despite only 28x28 pixels, variations in digit appearance gives considerable depth to the data (example digit '5' above).
The bad thing about MNIST is that it’s largely “solved” by supervised learning algorithms. A range of different supervised techniques have reached human performance and it’s debatable whether any further improvements are genuine.
So what’s the point of trying new approaches? Well, supervised algorithms have some odd qualities, perhaps due to the narrowness of training samples or the specificity of the cost function. For example, the discovery of “adversarial examples” - images that look easily classifiable to the naked eye but cannot be classified correctly with a trained network because they exploit weaknesses in trained neural networks.
But the biggest drawback of supervised learning is the need to tell it the “correct” answer for every input. This has led to a range of techniques - such as transfer learning - to make the most of what training data is available, even if not directly relevant. But fundamentally, supervised learning is unlike the experience of an agent learning as it explores its world. Animals can learn without a tutor.
However, unsupervised results with MNIST are less widely reported. Partially this is because you need to come up with a way to measure the performance of an unsupervised method. The most common approach is to use unsupervised networks to boost the performance of a final supervised network layer - but in MNIST the supervised layer is so powerful it’s hard to distinguish the contribution of the unsupervised layers. Nevertheless, these experiments are encouraging because having a few unsupervised layers seems to improve overall performance, compared to all-supervised networks. In addition to the limited data problem with supervised learning, unsupervised learning actually seems to add something.
One possible method of capturing the contribution of unsupervised layers alone is the Rand Index, which measures the similarity between two clusters. However, we are intending to use a distributed representation where there will be overlap between similar representations - that’s one of the features of the algorithm!
So, for now we’re going to go for the simplest approach we can think of, and measure the correlation between the active cells in selected hidden layers and each digit label, and see if the correlation alone is enough to pick the right label given a set of active cells. If the concepts defined by the digits exist somewhere in the hierarchy, they should be detectable as features uniquely correlated with specific labels...
Note also that we’re not doing any preprocessing of the MNIST images except binarization at threshold 0.5. Since the MNIST dataset is very high contrast, hopefully the threshold doesn’t matter much: It’s almost binary already.
See here and here to understand the classification role, and here for more information about prediction. Taken together, the ability to classify and predict future classifications allows sequences of input to be learned. This is a topic we have looked at in detail in earlier blog posts and we have some fairly effective techniques at our disposal.
We completed the following tests:
After completion of the unit tests we were satisfied that our Region-Layer component has the ability to efficiently produce variable order models of observed sequences using unsupervised learning, assuming that the states can reliably be detected.
We decided to run the following experiments:
Present each digit in the training set once, in a random order. Train the internal weights of the algorithm. Repeated several times if necessary.
Present each digit in the training set once, in a random order. Accumulate the frequency with which each active cell is associated with each digit label. After all images have been seen, convert the observed frequencies to correlations.
Present each digit in the testing set once, in a random order. Use the correlations between cell activity and training labels to predict the most likely digit label given the set of active cells in selected Region-Layer components (they are arranged into a hierarchy).
The motivation for this experiment is to see how the sequence learning can boost image recognition: Our Region-Layer component is supposed to be able to integrate both sequential and spatial information. This experiment actually has a lot of depth because English isn’t entirely predictable - if we use a different book for testing, there’ll be lots of sub-sequences the algorithm has never observed before. There’ll be uncertainty in image appearance and uncertainty in sequence, and we’d like to see how a hierarchy of Region-Layer components responds to both. Our expectation is that it will improve digit classification performance beyond the random image case.
In the next article, we will describe the specifics of the algorithms we implemented and tested on these problems.
A final article will present some results.
Results will be posted to the blog and written up for publication if, or when, we reach an acceptable level of novelty and rigor.
We are not trying to beat benchmarks here. We’re trying to show whether certain ideas have useful qualities - the best way to tackle specific AI problems is almost certainly not an AGI way. But what we’d love to see is that AGI-inspired methods can perform close to state-of-the-art (e.g. deep convolutional networks) on a wide range of problems. Now that would be general intelligence!
Dataset Choice
We are going to start with the MNIST digit classification dataset, and perform a number of experiments based on that. In future we will look at some more sophisticated image / object classification datasets such as LabelMe or Caltech_101.The good thing about MNIST is that it’s simple and has been extremely widely studied. It’s easy to work with the data and the images are a practical size - big enough to be interesting, but not so big as to require lots of preprocessing or too much memory. Despite only 28x28 pixels, variations in digit appearance gives considerable depth to the data (example digit '5' above).
The bad thing about MNIST is that it’s largely “solved” by supervised learning algorithms. A range of different supervised techniques have reached human performance and it’s debatable whether any further improvements are genuine.
So what’s the point of trying new approaches? Well, supervised algorithms have some odd qualities, perhaps due to the narrowness of training samples or the specificity of the cost function. For example, the discovery of “adversarial examples” - images that look easily classifiable to the naked eye but cannot be classified correctly with a trained network because they exploit weaknesses in trained neural networks.
But the biggest drawback of supervised learning is the need to tell it the “correct” answer for every input. This has led to a range of techniques - such as transfer learning - to make the most of what training data is available, even if not directly relevant. But fundamentally, supervised learning is unlike the experience of an agent learning as it explores its world. Animals can learn without a tutor.
However, unsupervised results with MNIST are less widely reported. Partially this is because you need to come up with a way to measure the performance of an unsupervised method. The most common approach is to use unsupervised networks to boost the performance of a final supervised network layer - but in MNIST the supervised layer is so powerful it’s hard to distinguish the contribution of the unsupervised layers. Nevertheless, these experiments are encouraging because having a few unsupervised layers seems to improve overall performance, compared to all-supervised networks. In addition to the limited data problem with supervised learning, unsupervised learning actually seems to add something.
One possible method of capturing the contribution of unsupervised layers alone is the Rand Index, which measures the similarity between two clusters. However, we are intending to use a distributed representation where there will be overlap between similar representations - that’s one of the features of the algorithm!
So, for now we’re going to go for the simplest approach we can think of, and measure the correlation between the active cells in selected hidden layers and each digit label, and see if the correlation alone is enough to pick the right label given a set of active cells. If the concepts defined by the digits exist somewhere in the hierarchy, they should be detectable as features uniquely correlated with specific labels...
Note also that we’re not doing any preprocessing of the MNIST images except binarization at threshold 0.5. Since the MNIST dataset is very high contrast, hopefully the threshold doesn’t matter much: It’s almost binary already.
Sequence Learning Tests
Before we start the experiments proper we conducted some ad-hoc tests to verify the features of the Region-Layer are implemented as intended. Remember, the Region-Layer has two key capabilities:- Classification … of the feedforward input, and
- Prediction … of future classification results (i.e. future internal states)
See here and here to understand the classification role, and here for more information about prediction. Taken together, the ability to classify and predict future classifications allows sequences of input to be learned. This is a topic we have looked at in detail in earlier blog posts and we have some fairly effective techniques at our disposal.
We completed the following tests:
- Cycle 0,1,2: We verified that the algorithm could predict the set of active cells in a short cycle of images. This ensures the sequence learning feature is working. The same image was used for each instance of a particular digit (i.e. there was no variation in digit appearance).
- Cycle 0,1,...,9: We tested a longer cycle. Again, the Region-Layer was able to predict the sequence perfectly.
- Cycle 0,1,2,3, 0,2,3,1: We tested an ambiguous cycle. At 0, it appears that the next state can be 1 or 2, and similarly, at 3, the next state can be 1 or 2. However, due to the variable order modelling behaviour of the Region-Layer, a single Region-Layer is able to predict this cycle perfectly. Note that first-order prediction cannot predict this sequence correctly.
- Cycle 0,1,2,3,1,2,4,0,2,3,1,2,1,5,0,3,2,1,4,5: We tested a complex graph of state sequences and again a single Region-Layer was able to predict the sequence perfectly. We also were able to predict this using only first order modelling and a deep hierarchy.
After completion of the unit tests we were satisfied that our Region-Layer component has the ability to efficiently produce variable order models of observed sequences using unsupervised learning, assuming that the states can reliably be detected.
Experiments
Now we come to the harder part. What if each digit exemplar image is ambiguous? In other words, what if each ‘0’ is represented by a randomly selected ‘0’ image from the MNIST dataset? The ambiguity of appearance means that the observed sequences will appear to be non-deterministic.We decided to run the following experiments:
Experiment 1: Random image classification
In this experiment there will be no predictable sequence; each digit must be recognized solely based on its appearance. The classic experiment is used: Up to N training passes over the entire MNIST dataset, followed by fixing the internal weights and a single pass to calculate the correlation between each active cell in selected hidden layer[s] and the digit labels. Then, a single pass over the test set recording, for each test input image, the most highly correlated digit label for each set of active hidden cells. The algorithm gets a “correct” result if the most correlated label is the correct label.- Passes 1-N: Train networks
Present each digit in the training set once, in a random order. Train the internal weights of the algorithm. Repeated several times if necessary.
- Pass N+1: Measure correlation of hidden layer features with training images.
Present each digit in the training set once, in a random order. Accumulate the frequency with which each active cell is associated with each digit label. After all images have been seen, convert the observed frequencies to correlations.
- Pass N+2: Predict label of test images.
Present each digit in the testing set once, in a random order. Use the correlations between cell activity and training labels to predict the most likely digit label given the set of active cells in selected Region-Layer components (they are arranged into a hierarchy).
Experiment 2: Image classification & sequence prediction
What if the digit images are not in a random order? We can use the English language to generate a training set of digit sequences. For example, we can get a book, convert each character to a 2 digit number and select random appropriate digit images to represent each number.The motivation for this experiment is to see how the sequence learning can boost image recognition: Our Region-Layer component is supposed to be able to integrate both sequential and spatial information. This experiment actually has a lot of depth because English isn’t entirely predictable - if we use a different book for testing, there’ll be lots of sub-sequences the algorithm has never observed before. There’ll be uncertainty in image appearance and uncertainty in sequence, and we’d like to see how a hierarchy of Region-Layer components responds to both. Our expectation is that it will improve digit classification performance beyond the random image case.
In the next article, we will describe the specifics of the algorithms we implemented and tested on these problems.
A final article will present some results.