 |
| Figure 1: The Region-Layer component. The upper surface in the figure is the Region-Layer, which consists of Cells (small rectangles) grouped into Columns. Within each Column, only a few cells are active at any time. The output of the Region-Layer is the activity of the Cells. Columns in the Region-Layer have similar - overlapping - but unique Receptive Fields - illustrated here by lines joining two Columns in the Region-Layer to the input matrix at the bottom. All the Cells in a Column have the same inputs, but respond to different combinations of active input in particular sequential contexts. Overall, the Region-Layer demonstrates self-organization at two scales: into Columns with unique receptive fields, and into Cells responding to unique (input, context) combinations of the Column's input. |
Introducing the Region-Layer
From our background reading (see here, here, or here) we believe that the key component of a general intelligence can be described as a structure of “Region-Layer” components. As the name suggests, these are finite 2-dimensional areas of cells on a surface. They are surrounded by other Region-Layers, which may be connected in a hierarchical manner; and can be sandwiched by other Region-Layers, on parallel surfaces, by which additional functionality can be achieved. For example, one Region-Layer could implement our concept of the Objective system, another the Region-Layer the Subjective system. Each Region-Layer approximates a single Layer within a Region of Cortex, part of one vertex or level in a hierarchy. For more explanation of this terminology, see earlier articles on Layers and Levels.
The Region-Layer has a biological analogue - it is intended to approximate the collective function of two cell populations within a single layer of a cortical macrocolumn. The first population is a set of pyramidal cells, which we believe perform a sparse classifier function of the input; the second population is a set of inhibitory interneuron cells, which we believe cause the pyramidal cells to become active only in particular sequential contexts, or only when selectively dis-inhibited for other purposes (e.g. attention). Neocortex layers 2/3 and 5 are specifically and individually the inspirations for this model: Each Region-Layer object is supposed to approximate the collective cellular behaviour of a patch of just one of these cortical layers.
We assume the Region-Layer is trained by unsupervised learning only - it finds structure in its input without caring about associated utility or rewards. Learning should be continuous and online, learning as an agent from experience. It should adapt to non-stationary input statistics at any time.
The Region-Layer should be self-organizing: Given a surface of Region-Layer components, they should arrange themselves into a hierarchy automatically. [We may defer implementation of this feature and initially implement a manually-defined hierarchy]. Within each Region-Layer component, the cell populations should exhibit a form of competitive learning such that all cells are used efficiently to model the variety of input observed.
We believe the function of the Region-Layer is best described by Jeff Hawkins: To find spatial features and predictable sequences in the input, and replace them with patterns of cell activity that are increasingly abstract and stable over time. Cumulative discovery of these features over many Region-Layers amounts to an incremental transformation from raw data to fully grounded but abstract symbols.
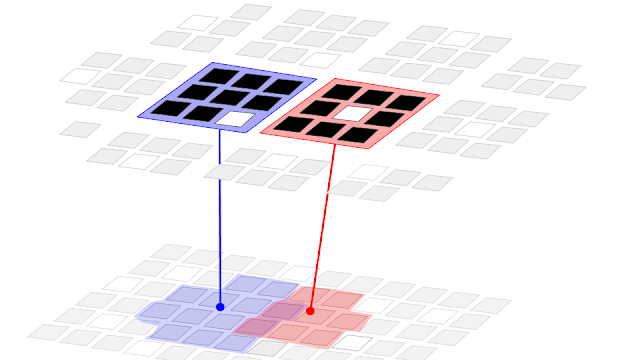
Within a Region-Layer, Cells are organized into Columns (see figure 1). Columns are organized within the Region-Layer to optimally cover the distribution of active input observed. Each Column and each Cell responds to only a fraction of the input. Via these two levels of self-organization, the set of active cells becomes a robust, distributed representation of the input.
Given these properties, a surface of Region-Layer components should have nice scaling characteristics, both in response to changing the size of individual Region-Layer column / cell populations and the number of Region-Layer components in the hierarchy. Adding more Region-Layer components should improve input modelling capabilities without any other changes to the system.
So let's put our cards on the table and test these ideas.
Region-Layer Implementation
Parameters
For the algorithm outlined below very few parameters are required. The few that are mentioned are needed merely to describe the resources available to the Region-Layer. In theory, they are not affected by the qualities of the input data. This is a key characteristic of a general intelligence.
- RW: Width of region layer in Columns
- RH: Height of region layer in Columns
- CW: Width of column in Cells
- CH: Height of column in Cells
Inputs and Outputs
- Feed-Forward Input (FFI): Must be sparse, and binary. Size: A matrix of any dimension*.
- Feed-Back Input (FBI): Sparse, binary Size: A vector of any dimension
- Prediction Disinhibition Input (PDI): Sparse, rare. Size: Region Area+
- Feed-Forward Output (FFO): Sparse, binary and distributed. Size: Region Area+
* the 2D shape of input[s] may be important for learning receptive fields of columns and cells, depending on implementation.
+ Region Area = CW * CH * RW * RH
Pseudocode
Here is some pseudocode for iterative update and training of a Region-Layer. Both occur simultaneously.
We also have fully working code. In the next few blog posts we will describe some of our concrete implementations of this algorithm, and the tests we have performed on it. Watch this space!
function: UpdateAndTrain(
feed_forward_input,
feed_back_input,
prediction_disinhibition
)
// if no active input, then do nothing
if( sum( input ) == 0 ) {
return
}
// Sparse activation
// Note: Can be implemented via a Quilt[1] of any competitive learning algorithm,
// e.g. Growing Neural Gas [2], Self-Organizing Maps [3], K-Sparse Autoencoder [4].
activity(t) = 0
for-each( column c ) {
// find cell x that most responds to FFI
// in current sequential context given:
// a) prior active cells in region
// b) feedback input.
x = findBestCellsInColumn( feed_forward_input, feed_back_input, c )
activity(t)[ x ] = 1
}
// Change detection
// if active cells in region unchanged, then do nothing
if( activity(t) == activity(t-1) ) {
return
}
// Update receptive fields to organize columns
trainReceptiveFields( feed_forward_input, columns )
// Update cell weights given column receptive fields
// and selected active cells
trainCells( feed_forward_input, feed_back_input, activity(t) )
// Predictive coding: output false-negative errors only [5]
for-each( cell x in region-layer ) {
coding = 0
if( ( activity(t)[x] == 1 ) and ( prediction(t-1)[x] == 0 ) ) {
coding = 1
}
// optional: mute output from region, for attentional gating of hierarchy
if( prediction_disinhibition(t)[x] == 0 ) {
coding = 0
}
output(t)[x] = coding
}
// Update prediction
// Note: Predictor can be as simple as first-order Hebbian learning.
// The prediction model is variable order due to the inclusion of sequential
// context in the active cell selection step.
trainPredictor( activity(t), activity(t-1) )
prediction(t) = predict( activity(t) )
[2] https://papers.nips.cc/paper/893-a-growing-neural-gas-network-learns-topologies.pdf
[3] http://www.cs.bham.ac.uk/~jxb/NN/l16.pdf
[4] https://arxiv.org/pdf/1312.5663
[5] http://www.ncbi.nlm.nih.gov/pubmed/10195184
No comments :
Post a Comment